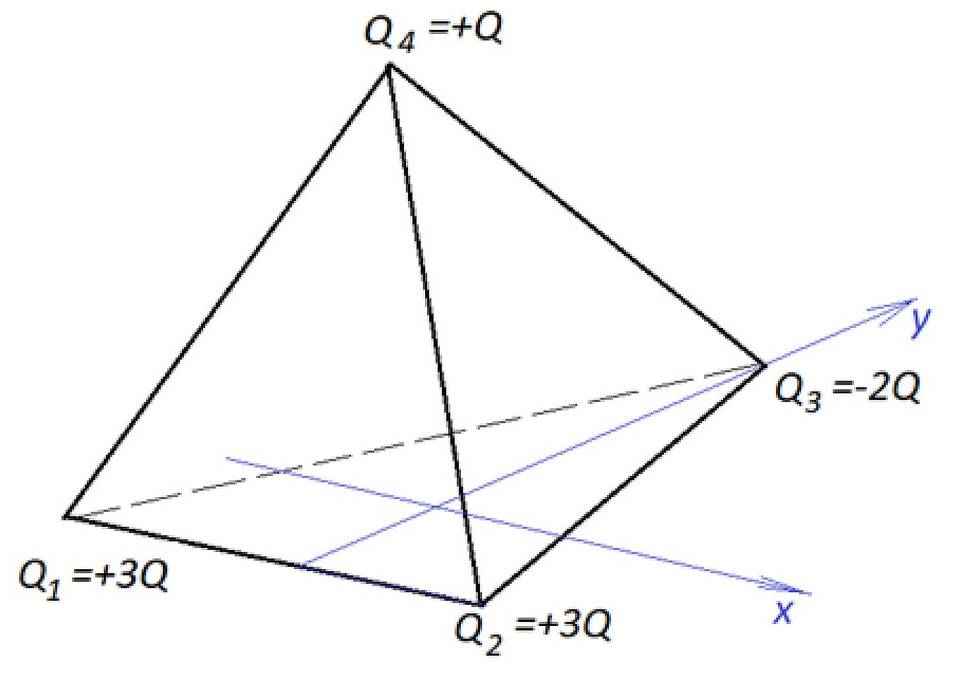
Тетраэдр - это многогранник с четырьмя треугольными гранями, шестью рёбрами и четырьмя вершинами. Это простейший вид пирамиды и трёхмерный аналог треугольника.
Содержание
Определение тетраэдра
Виды углов в тетраэдре
| Тип угла | Описание |
| Плоские углы | Углы между рёбрами на каждой грани (всего 12) |
| Двугранные углы | Углы между смежными гранями (всего 6) |
| Телесные углы | Углы при вершинах (всего 4) |
Сумма плоских углов
Для каждой треугольной грани:
Сумма внутренних углов любого треугольника равна π радиан (180°). Поскольку тетраэдр имеет 4 грани:
- Общая сумма всех плоских углов: 4 × π = 4π (720°)
- Однако это включает внешние углы при вершинах
Правильный тетраэдр:
Все грани - равносторонние треугольники с углами по π/3 (60°):
12 × π/3 = 4π (720°)
Сумма двугранных углов
Для любого тетраэдра сумма двугранных углов удовлетворяет соотношению:
Σαi = 2π + Ω
где Ω - полный избыток тетраэдра (аналог сферического избыкта)
| Тип тетраэдра | Сумма двугранных углов |
| Правильный | ≈ 2.03π (366°) |
| Ортоцентрический | 2π (360°) |
Телесные углы при вершинах
Сумма телесных углов Ωi в тетраэдре связана с его двугранными углами αij формулой:
Ω = Σ(αij + αik + αil - π)
Для правильного тетраэдра:
- Телесный угол при вершине: ≈ 0.551 стерадиан
- Сумма всех телесных углов: ≈ 2.204 стерадиан
Связь с топологией
Суммы углов тетраэдра связаны с его топологическими характеристиками:
- Эйлерова характеристика: V - E + F = 2
- Гаусс-Бонне: ∫KdA + Σεi = 2πχ
- Дефект углов: δ = 2π - Σθ
Геометрические свойства:
| Свойство | Значение |
| Объём через углы | Формула Синайяра |
| Радиус описанной сферы | Через телесные углы |
Историческая справка:
Изучение угловых характеристик тетраэдра началось с работ Эйлера и Гаусса, современная теория развита в работах по дифференциальной геометрии.